November 4, 2020 17 min to read

The Theorem and Practice to Make an Unity3D Audio Visualizer

Using GetSpectrumData function of Unity3D to make an audio visulizer.

Terminologies
The Unity GetSpectrumData function
The spectrum data and the Fourier transform
The audio visulizer

Terminologies

Sound: In the aspect of physics, the sound is a sort of wave that viberats in the air with a frequency between 20Hz and 20000Hz.
Sound Frequency: The sound frequency is the times of the sound’s vibration per second. It’s unit is herz.
Sampling: In this article, sampling means to get a sample, a value, from a sound wave.
Sampling Rate: Sampling rate is the times of the Sampling per second.
Fast Fourier Transform: Abbreviated as FFT, it is a math function that can be used to transform signals.
Window Function: An variable of the FFT function, it can be used to reduce the “signal to noise ratio”.
Decibel: It is a well-known value to measure sound’s volume. However, in this article, the strength of the sound wave is a relative value and has nothing to do with the decibel.

The Unity GetSpectrumData function

public void GetSpectrumData(float[] samples, int channel, FFTWindow window);

samples: The array is the return value of the funciton. Each element’s value is the strength of the audio source at a certain frequency. To be optimized for the Fourier transform algorithm, the length of the array must be the power of two, minimal 64 and maximum 8192.
channel: Nowadays audio hardware system has more than one speaker. The mechanism of seperating an audio into different parts, also called channels, and then providing them to different speakers to play is called steoro. On the contrast, all speakers playing the same audio is called Mono. In the case of steoro, the channel parameter is used to choose a certain channel of the audio to sample. Normally this parameter should be set to 0 (Mono mode) to sample all channels. window: This parameter decides the helper function for the FFT to reduce noises. There is a trade-off between the complexity of the window-function and noises reducing performance. usage:

public float[] spectrumData=new float[8192];  
thisAudioSource.GetSpectrumData(spectrumData,0,FFTWindow.BlackmanHarris);  

The spectrum data and the Fourier transform

Given the sampling time T, the samples N and the sampling rate $f_s$, we can make a formula: $T=N/f_s$.

The reciprocal of T, which is $f_s/N$, is called Frequency Resolution. The charts below are the results of the FFT of the demo audio in low/high Frequency Resolution. It is clear to see that the higher the Frequency Resolution the denser the data transformed.

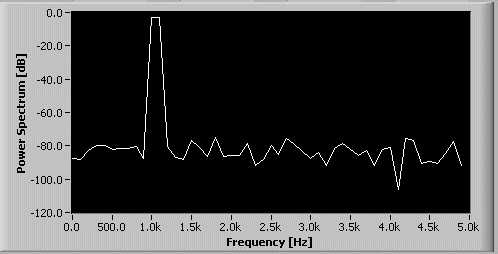
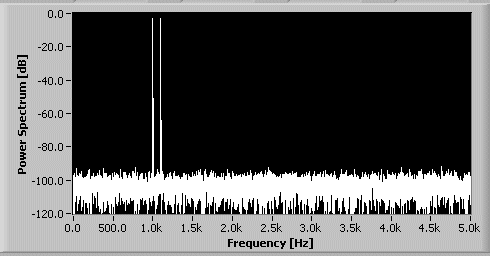
The length of the spectrumData array that is returned by the GetSpectrumData is actually the Frequency Resolution and the array’s each element’s value represents a y/x value in the diagrams above. Unfortunately, it is unclear whether these values are the power spectrums or the powers at a given frequency but it is good enough most of the time as long as they are relative numbers.

Another problem is that the information about the representing frequency of the array’s element is unwritten in the Unity’s documentation or C# source code. Determinating the frequency is vital at runtime. So let’s try to figure it out through some tests.

Using a software to analyze “[MV] FIESTAR(피에스타) _ Mirror.mp3”, we can see that there is a free fall of the wave around the 16000Hz frequency.

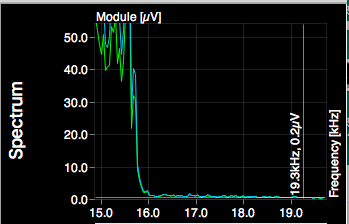
Back to Unity, debugging the spectrum-data shows a significant decrease of value at spectrumData[5500]. Therefore, it can be deduced that the spectrumData[5500] represences the frequency around 16000Hz. Moreover, because 16000Hz/5500*8192=23831Hz, so another conclusion is that the highest possible frequency of the specturm-data is between 22000Hz to 24000Hz.

In addtion to the tests, other clues can be found from the angle of the Fourier Transform. The core algorithm of GetSpectrumData function is the FFT. As mentioned in the beginning, sounds can be seen as waves where wave’s frequency decided sound’s pitch and amplitude determined volume.

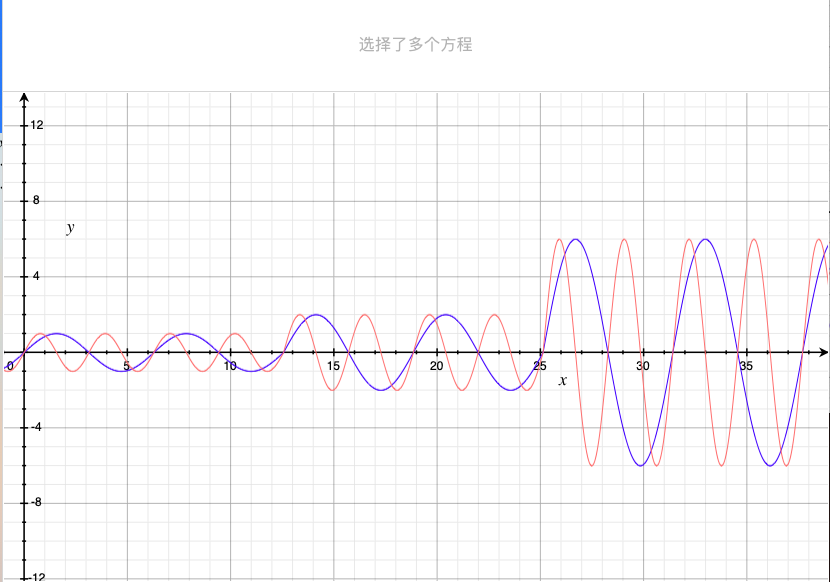
The graph above shows the two sound waves with the stable frequency and gradually amplified amplitude in the x-time/y-amplitude plane. According to the superposition principle, simply adding these waves will generate a new complex wave.

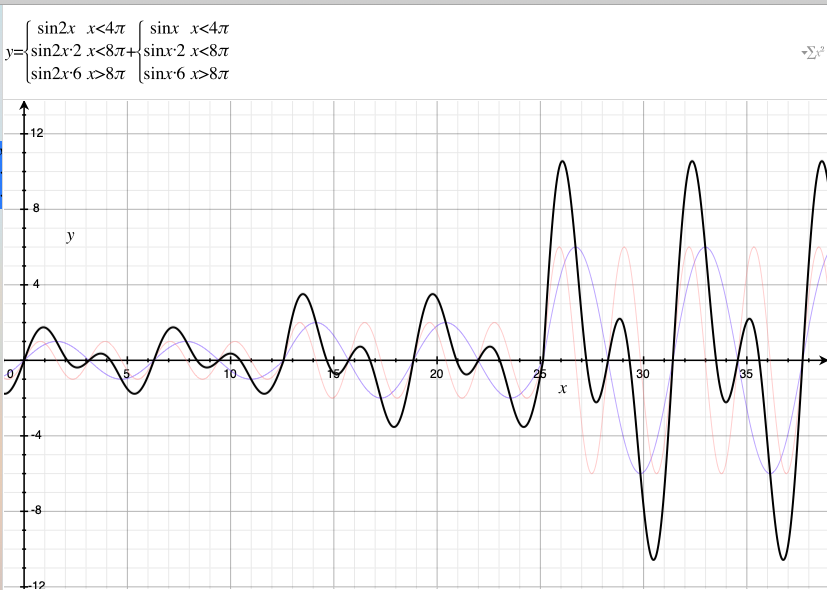
This is exactly what happend when the different sound waves met in the air to create a mixed tone. The data of a audio file are just the discrete samples of a complex sound wave. From this perspective, we can say that making audio/music is adding different sound waves into a complex wave. Just the opposite, the Fourier Transform breaks down the complex wave to simple waves. No matter how complex the wave is, through a series of magical calculations(much more complicated than those to mix them), the FT can identify every single-frequency wave within it.

From the viewpoint of the two-dimensional space, the Fourier Transform will translate the complex wave from the “x-time/y-amplitude” plane(the last chart above) to the “x-frequency/y-power”(e.g the third graph of this article) and then to multiple “x-time/y-power of a single wave” planes with different frequency. Finally, every y (power of a single wave) information saves to the elements of the spectrumData array in order of it’s frequency.

In this transfomation process, firstly, the FFT samples the original complex wave on the time axis repeatedly with a constant interval. To correctly reconstruct the single-frequency wave, sufficient samples are necessary. And here comes “the Nyquist–Shannon sampling theorem”. To put it simply, the theorem states that the number of the sufficient samples is the frequency multiply by two. For instance, 3Hz wave needs 6 samples.

The standard sampling rate of nowadays music industry is 44100Hz. In other words, one second of a music audio file contains 44100 samples. According to the Nyquist theorem, the highest frequency of a single wave the FFT can correctly reconstruct is 22050Hz, which is consistent with the conclusion of the tests above.

Given the highest frequency and the length of the spectrumData array, now we can further determine the exact frequencies of each element of the array. For example, the demo project of this article has used a 8192 array:

spectrumData[0] <=> 22050Hz/8192*1 = 2.6916 Hz <=> 6 times sampling per second
spectrumData[1] <=> 22050Hz/8192*2 = 5.3833 Hz <=> 11 times sampling per second
…
spectrumData[8191] <=> 22050Hz/8192*8192 = 22050 Hz <=> 44100 times sampling per second

The table clearly shows another conclusion, the longer the array the more the sampling and thus the more performance cost of the GetSpectrumData function.

Adjusting the length of the array, many frequency’s strength can be obtained. Hence the analyze can be extended to a wider range, e.g grabing the pitchs of music.

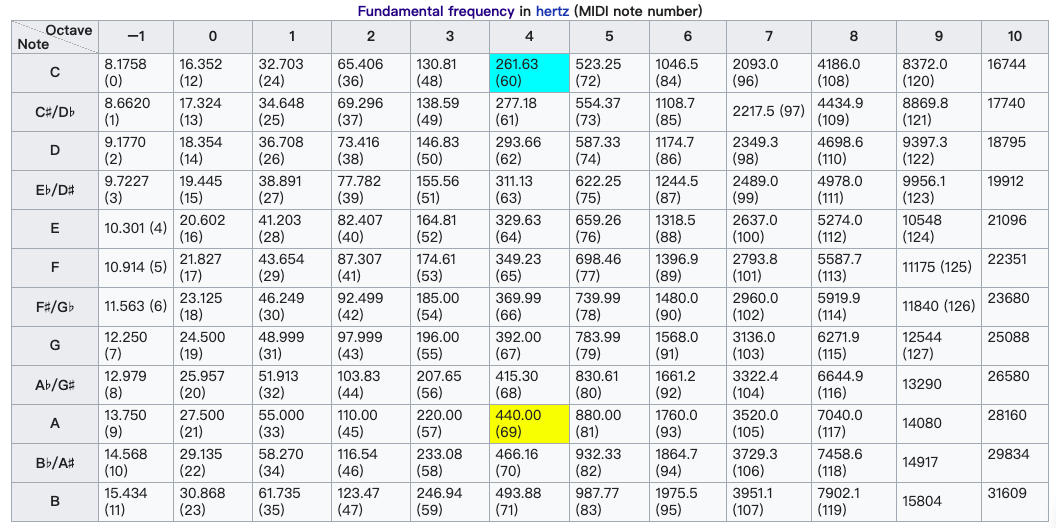
According to this pitch/frequncy table, the highest pitch’s frequncy of octave 9 is 15804Hz. This explains the phenomenon of the free fall around 16000Hz of the FFT of the song in the above test.

The audio visulizer

The Github Link of the demo project

In the demo project, I obtain the spectrum data in Update and inject them to the scales of the cubes and the colors of cubes’ materials. The workload is distributed to both CPU and GPU. If you want to reduce the burden of CPU, another idea is to translate the whole spectrum data, the array, to the GPU(since you have to use this bandwidth to set colors anyway) and then to hand over all the work, like vertex animation, color calculation and etc, to shaders. Using the vertex or fragment shader to calculate colors instead of CPU is also more friendly for batching, which could reduce a lot of SetPass calls.

Since the highest meaningful frequncy of the song is below 16000Hz, the audio visualizer only uses 5461 cubes.

The core logic of the demo is in the Controller script:

using UnityEngine;
using System.Collections;
using DG.Tweening;

public class Controller : MonoBehaviour {
    //audio related
    public AudioSource thisAudioSource;
    private float[] spectrumData = new float[8192];
    //cube related
	public GameObject cubePrototype;
	public Transform startPoint;
	private Transform[] cube_transforms=new Transform[8192];
    private Vector3[] cubes_position= new Vector3[8192];
    //color related
    public GridOverlay gridOverlay;
    private MeshRenderer[] cube_meshRenderers = new MeshRenderer[8192];
    private bool cubeColorChange;
    private bool gridColorChange;
    //camera movement related
    public Vector3 cameraStartPoint;
    public Transform cameraTransform;
    public bool lookat0_1;
    public bool lookat1_2;
    public bool lookat2_3;
    public Vector3 lookat0_1_vector = Vector3.zero;
    public Vector3 lookat1_2_vector = new Vector3(106f, 12f, 78f);
    public Vector3 lookat2_3_vector = Vector3.zero;
    private Vector3[] moveTos = new Vector3[8192];
    public Transform cubes_parent;
    private bool cubesRotate = true;
	// Use this for initialization
	void Start () {
        //cube generation
		Vector3 p=startPoint.position;

		for(int i=0;i<8192;i++){
			p=new Vector3(p.x+0.11f,p.y,p.z);
            GameObject cube=Object.Instantiate(cubePrototype,p,cubePrototype.transform.rotation)as GameObject;
			cube_transforms[i]=cube.transform;
            cube_meshRenderers[i] =cube.GetComponent<MeshRenderer>();
		}

		p=startPoint.position;

		float a=2f*Mathf.PI/5461;

		for(int i=0;i<5461;i++){
			cube_transforms[i].position=new Vector3(p.x+Mathf.Cos(a)*131,p.y,p.z+131*Mathf.Sin(a));
			a+=2f*Mathf.PI/5461;
            cubes_position[i]=cube_transforms[i].position;
			cube_transforms[i].parent=startPoint;
		}
        //manage color
        gridColorChange = false;
        cubeColorChange = false;
        Invoke("SwitchCC", 3f);
        //manage camera
        cameraStartPoint = cameraTransform.position;
        StartCoroutine(CameraMovement());
        //delay the music
        thisAudioSource.PlayDelayed(2f);
	}
	// Update is called once per frame
	void Update () {
        Spectrum2Cube();
        DynamicColor();
        CameraLookAt();
	}
	//color related
    void SwitchCC(){
        cubeColorChange = !cubeColorChange;
    }
    void SwitchGC(){
        gridColorChange = !gridColorChange;
    }
	void DynamicColor(){
        if (cubeColorChange)
        {
            for (int i = 0; i < 5461; i++)
            {
                cube_meshRenderers[i].material.SetColor("_Color", new Vector4(Mathf.Lerp(cube_meshRenderers[i].material.color.r, spectrumData[i] * 500f, 0.2f), 0.5f, 1f, 1f));
            }
        }
        if (gridColorChange)
        {
            float gridColor = Mathf.Lerp(gridOverlay.mainColor.r, spectrumData[2000] * 1000, 0.5f);
            if (gridColor > 1)
            {
                gridColor = 1;
            }
            gridOverlay.mainColor = new Vector4(gridColor, 0.5f, 1f, 1f);
        }
    }
    //inject spectrumData to the scale of the cubes
    void Spectrum2Cube(){
        thisAudioSource.GetSpectrumData(spectrumData, 0, FFTWindow.BlackmanHarris);
        for (int i = 0; i < 5461; i++)
        {
            cube_transforms[i].localScale = new Vector3(0.15f, Mathf.Lerp(cube_transforms[i].localScale.y, spectrumData[i] * 10000f, 0.5f), 0.15f);
        }
    }
    //manage the angles of the camera
    void CameraLookAt(){
        if (lookat0_1)
        {
            cameraTransform.LookAt(lookat0_1_vector);
        }
        if (lookat1_2)
        {
            cameraTransform.LookAt(lookat1_2_vector);

        }
        if (lookat2_3)
        {
            cameraTransform.LookAt(cubes_position[5190]);
        }
    }
    //animate the grid
    IEnumerator GridOff()
    {
        for (int i = 0; i < 51; i++)
        {
            gridOverlay.largeStep += 10;
            yield return new WaitForSeconds(0.02f);
        }
        gridOverlay.showMain = false;

    }
    IEnumerator GridOn()
    {
        gridOverlay.showMain = true;
        gridColorChange = true;
        gridOverlay.largeStep = 500;
        for (int i = 0; i < 49; i++)
        {
            gridOverlay.largeStep -= 10;
            yield return new WaitForSeconds(0.02f);
        }
    }
    //repeat the camera movement. TODO: exit mechanism
    public void CameraRepeatMove()
    {
        StopAllCoroutines();
        StartCoroutine(CameraMovement());
        if (cubesRotate)
        {
            cubesRotate = false;
            cubes_parent.DORotate(new Vector3(0f, 360f, 0f), 117f, RotateMode.FastBeyond360);
        }
        gridColorChange = false;
    }
    //move the camera
    IEnumerator CameraMovement()
    {
        yield return new WaitForSeconds(20f);
        lookat2_3_vector = new Vector3(cubes_position[5200].x, 12f, cubes_position[5200].z);
        cameraTransform.DOMove(startPoint.position, 20f);
        for (int i = 0; i < 8192; i++)
        {
            moveTos[i] = new Vector3(cubes_position[i].x, 10f, cubes_position[i].z);
        }
        yield return new WaitForSeconds(20f);
        cameraTransform.DOMove(new Vector3(126f, 252f, 1f), 10f);
        cameraTransform.DOLookAt(Vector3.zero, 10f, AxisConstraint.None, Vector3.up);
        yield return new WaitForSeconds(10f);
        cameraTransform.DOMove(new Vector3(106f, 12f, 78f), 19f);
        cameraTransform.DOLookAt(lookat1_2_vector, 19f, AxisConstraint.None, Vector3.up);
        yield return new WaitForSeconds(19f);
        lookat1_2 = false;
        StartCoroutine(GridOn());
        cameraTransform.DOLookAt(lookat2_3_vector, 8f, AxisConstraint.None, Vector3.up);
        cameraTransform.DOMove(new Vector3(cubes_position[5460].x, 12f, cubes_position[5460].z), 8f);
        yield return new WaitForSeconds(8f);
        cameraTransform.DOLookAt(cubes_position[5200], 2f, AxisConstraint.None, Vector3.up);
        yield return new WaitForSeconds(2f);
        int counter = 0;
        while (counter < 2700)
        {
            cameraTransform.LookAt(cubes_position[5200 - counter]);
            cameraTransform.DOMove(moveTos[5460 - counter], 0.01f);
            yield return new WaitForSeconds(0.01f);
            counter += 10;
        }
        cameraTransform.DOLookAt(lookat0_1_vector, 3f, AxisConstraint.None, Vector3.up);
        yield return new WaitForSeconds(3f);
        StartCoroutine(GridOff());
        lookat0_1 = true;
        cameraTransform.DOMove(new Vector3(cameraStartPoint.x, cameraStartPoint.y + 300f, cameraStartPoint.z), 6f);
        yield return new WaitForSeconds(6f);
        lookat0_1 = false;
        CameraRepeatMove();
    }
} 